
Vol. 4 | No. 8 | Agosto 2024 - enero 2025 | ISSN: 3006-1385 | ISSN-L: 3006-1385 | Pág. 49 – 61
El constructivismo y las tecnologías para favorecer la enseñanza aprendizaje de la matemática en el Bachillerato
Constructivism and technologies to promote the teaching and learning of mathematics in high school
Marco Vinicio Cuyo Sigcha
http://orcid.org/0000-0002-8246-2860
Unidad Educativa “Narciso Cerda Maldonado”, Cotopaxi, Ecuador.
Artículo recibido 16 de marzo de 2024 / Arbitrado 18 de abril de 2024/ Aceptado 26 de junio 2024 / Publicado 30 de agosto de 2024
http://doi.org/10.62319/simonrodriguez.v.4i8.33
![]()
RESUMEN
El constructivismo se centrado en el estudiante como participante activo de su formación, dotado de las herramientas necesarias para resolver diversas situaciones problemáticas. Frente al desafío por obtener mejores resultados en el aprendizaje de los educandos, en la presente investigación se realiza un análisis respecto a si favorece el enfoque constructivista y el empleo de las herramientas tecnológicas, el proceso de enseñanza – aprendizaje de la matemática en el bachillerato. Al analizarse las teorías sobre el aprendizaje constructivista y la concepción del alineamiento constructivo, se considera que la aplicación en esta disciplina, unido al uso de las tecnologías, produciría grandes beneficios al proceso formativo, lo cual se acredita con la evidencia de los resultados obtenidos por varios autores. Se concluye, que esta metodología podría resultar favorable para lograr en los estudiantes un aprendizaje significativo, lo que les permitiría comprender, aprender, recordar y aplicar mejor los conceptos matemáticos.
Palabras clave: aprendizaje activo; aprendizaje significativo; constructivismo; enfoque constructivista; estudiantes bachillerato; herramientas tecnológicas.
ABSTRACT
Constructivism focuses on the student as an active participant in his or her training, equipped with the necessary tools to solve various problematic situations. Faced with the challenge of obtaining better results in the learning of students, in this research an analysis is carried out regarding whether the constructivist approach and the use of technological tools favors the teaching-learning process of mathematics in high school. When analyzing the theories on constructivist learning and the conception of constructive alignment, it is considered that the application in this discipline, together with the use of technologies, would produce great benefits to the training process, which is accredited with the evidence of the results obtained by several authors. It is concluded that this methodology could be favorable for achieving meaningful learning in students, which would allow them to better understand, learn, remember and apply mathematical concepts.
Keywords: active learning; significant learning; constructivism; constructivist approach; high school students; technological tools.
INTRODUCCIÓN
La matemática es fundamental para el desarrollo de las habilidades cognitivas, lógico y analítico; así como en la adquisición de habilidades numéricas, espaciales y abstractas. Li y Schoenfeld (2019) consideran que son muchos los beneficios que brinda, su aprendizaje en términos de razonamiento lógico, resolución de problemas y toma de decisiones. Martínez et al. (2023), coincide con esto al pensar que cada concepto matemático tiene una aplicación directa, desde el cálculo hasta la geometría avanzada.
Entre tanto, se coincide con Esquivel (2023), en que matemática es considerada una materia difícil, lo que ocasiona de manera frecuente bajos índices de motivación y actitudes negativas hacia el aprendizaje de los contenidos. Como consecuencia a esto, los estudiantes pueden tener bajo rendimiento académico. El proceso formativo se puede tornar más complejo si se le suma, que el profesorado muchas veces aplica en su práctica pedagógica métodos tradicionales en los cuales los alumnos son simples receptores de clases, que memorizan conceptos matemáticos y lecciones sin llegar a su comprensión.
En el caso de los estudiantes de bachillerato que abarca de los 13 a los 16 años aproximadamente, como menciona la teoría Piaget con las cuatro etapas del desarrollo cognitivo, los jóvenes se encuentran en la cuarta etapa de operaciones formales: “el adolescente, pensador formal, está cognitivamente equipado para desarrollar planteamientos de experimentación complejos, plantear hipótesis y controlar inteligentemente las variables involucradas para poder comprobarlas o refutarlas” (Contreras, 2021, p.5). A pesar de esto, muchos jóvenes presentan dificultades para comprender la matemática por lo descrito anteriormente.
En un contexto educativo desafiante como este, donde los alumnos pueden sentirse desmotivados, existe el enfoque pedagógico constructivista que busca fomentar un aprendizaje interactivo y estimulante. El constructivismo es un método de enseñanza que al decir Miranda (2022), se centra en que el estudiante es protagonista de su aprendizaje y realiza una construcción activa de su conocimiento, basándose en sus experiencias previas; para ello establece una interacción con el docente, donde cada uno expresa su conocimiento para alcanzar un aprendizaje significativo.
En relación al constructivismo, Miranda (2020), considera que enseñar y aprender matemática se sustenta en permitir a los estudiantes desarrollar las habilidades numéricas de modo que puedan aplicarlo en la vida cotidiana; además de requerir que el docente realice una praxis que guíe a los alumnos en su proceso educativo. Por consiguiente, Gómez y Pérez (2023), pudo demostrar que con la aplicación de las metodologías activas aplicadas en la enseñanza de esta asignatura, los estudiantes aprenden de manera más óptima, duradera e influye directamente en su rendimiento académico.
Unido al empleo del enfoque constructivista, la incorporación de recursos, aplicaciones y medios informáticos constituyen recursos valiosos que enriquecen el proceso de enseñanza-aprendizaje de la matemática. Las Tecnologías de la Información y las Comunicaciones (TIC) ofrecen una amplia gama de posibilidades, desde presentaciones multimedia, simulaciones interactivas, juegos educativos, hasta plataformas de aprendizaje en línea. Estas herramientas digitales ayudan a captar la atención de los educandos, facilitan la compresión de procedimientos complejos y promueven la colaboración y el trabajo en equipo.
Al combinar el enfoque constructivista con el uso estratégico de las TIC, los docentes pueden crear entornos de aprendizaje dinámicos y motivadores, donde los estudiantes se sientan protagonistas de su propio proceso de aprendizaje. De esta manera, se fomenta el desarrollo de habilidades como el pensamiento crítico, la creatividad y la capacidad de resolver problemas, lo que los prepara para enfrentar los desafíos del mundo actual.
Ante estos beneficios y al considerar los desafíos que tiene el proceso formativo de la matemática, es válido preguntarse: ¿Favorece el enfoque pedagógico constructivista y el empleo de las herramientas tecnológicas, el proceso de enseñanza – aprendizaje de la matemática en el bachillerato?
DESARROLLO
Para el desarrollo de la presente investigación sobre la manera en que favorecería el enfoque pedagógico constructivista y los recursos TIC en la enseñanza – aprendizaje de la matemática en el bachillerato, se precisa la comprensión de algunos elementos claves del constructivismo. Para ello, se debe tener en cuenta que el constructivista se enfoca en promover la resolución de problemas y el desarrollo de habilidades cognitivas. En su aplicación en esta materia, es necesario conocer la teoría del aprendizaje constructivista, la cual implica que los estudiantes deben construir de manera activa su propio conocimiento a través de la exploración y la práctica de conceptos, además de ser significativo y autónomo. Para una correcta concepción y aplicación de este enfoque, es necesario que exista un alineamiento constructivo entre el proceso de enseñanza-aprendizaje-evaluación. Entre tanto, unido a esta concepción, la incorporación de herramientas tecnológicas a los procesos educativos potencia aún más el proceso formativo con recursos que resultan motivadores y facilitan el aprendizaje, distintas investigaciones así lo corroboran.
Teorías sobre el aprendizaje constructivista
A lo largo de los tiempos diversas personas han planteado varias teorías sobre el aprendizaje constructivista, de ellas, la teoría del aprendizaje significativo de David Paul Ausubel, el paradigma socio-cultural de Lev Semiónovich Vigotsky y el paradigma psicogenético de Jean Piaget, se consideran más cercanos a los planteamientos del constructivismo.
Para David Paul Ausubel el aprendizaje es significativo, se basa en la recepción y el descubrimiento (Walter, et al. 2014). Para su logro es preciso tener en cuenta lo que el alumno ya sabe sobre lo que se le va a enseñar, puesto que el nuevo conocimiento se asentará sobre el viejo. El contenido de aprendizaje debe tener una estructura lógica y psicológica (Gutiérrez, 1987). Considera que aprender es sinónimo de comprender y que lo que se comprenda será lo que se aprenderá y recordará mejor porque quedará integrado en la estructura de conocimientos.
Desde la concepción de Lev Semiónovich Vigotsky el aprendizaje es un factor de desarrollo y su adquisición se explica cómo formas de socialización. Lo considera como un fenómeno que ocurre en una “zona de desarrollo próximo” (Hernández, 2015) en la cual el aprendiz puede resolver, con la ayuda de socios de aprendizaje más avanzados (mediadores), problemas más complejos de los que resolvería solo. Se debe tener en cuenta además que el aprendizaje es siempre la actividad del sujeto.
Jean Piaget por su parte, considera que el aprendizaje es el proceso mediante el cual el estudiante, como copartícipe activo de su propio conocimiento, lo estructura a partir de sus experiencias generadas (Parrat, 2012); es decir que no constituye una copia de la realidad, sino una construcción activa del sujeto en interacción con su entorno. Considera además, que está limitado por el nivel de desarrollo cognitivo del alumno y que se construye al ejercer acciones sobre el medio. Se hace visible lo que se va aprendiendo en desempeños que demuestren su uso en el logro de productos diversos (Raynaudo y Peralta, 2017).
Piaget además considera que, en el proceso de construir el conocimiento, se transita por diferentes estadios del desarrollo de la inteligencia de manera progresiva, según un procedimiento bien programado. Esta visión educativa se ubica a nivel psicológico, considerándose que la inteligencia procede de la acción. De ahí que Piaget (1949, p. 39) asegura que “el alumno debe experimentar activamente para reconstruir por sí mismo lo que ha de aprender; y que solo se aprende a experimentar probando uno mismo, trabajando activamente”. Es por ello que debe actuar de forma creativa para producir y no solo reproducir el conocimiento.
En este sentido, Saldarriaga, et al. (2016), al estudiar la teoría de Piaget descubrieron como para él, la inteligencia es producto del desarrollo espontáneo, que depende de cuatro factores principales: el desarrollo en término de crecimiento biológico y maduración psicológico; la experiencia, elemento importante para el desarrollo cognitivo; la transmisión social, que indica que ningún mensaje ni conducta nueva se incorpora al sujeto si éste no activa las estructuras previas adecuadas para procesarlo y asimilarlo; y el factor de equilibración, que permite la búsqueda interna de nuevos niveles y reorganizaciones de equilibrio mental, después de cada alteración cognoscitiva provocado desde el exterior o auto provocada.
Concepción efectiva del enfoque constructivista y alineamiento constructivo
Al aplicar el principio constructivista en el proceso de enseñanza - aprendizaje de la matemática, se debe proporcionar al alumno las herramientas que les permita crear sus propios procedimientos para resolver situaciones problemáticas, esto implica que sus ideas se modifiquen y siga aprendiendo. Para ello, la realización de tareas que exigen trabajo cooperativo constituyen según Navarro, et al. (2019), una alternativa más factible que la clase magistral y el estudio memorístico, porque consigue un adecuado rendimiento en la adquisición del conocimiento.
En la figura 1 se ha sintetizado y esquematizado los elementos fundamentales que algunos de los autores citados en la investigación han abordado sobre la concepción efectiva de la aplicación del enfoque constructivista. En este sentido, la enseñanza de la matemática busca promover un aprendizaje significativo y duradero. Los estudiantes no solo recuerdan fórmulas y procedimientos, sino que también comprenden el significado detrás de ellos. Con esta concepción los educandos deben participar de forma activa en la resolución de problemas y en la construcción de conceptos a través de la interacción con su entorno, esto contribuirá al desarrollo de las habilidades, el pensamiento crítico y la transferencia de conocimientos a situaciones reales. También se debe enfocar en potenciar la zona de desarrollo próximo de los educandos, en lo que se debe tener en cuenta sus conocimientos previos como base para el nuevo aprendizaje. Además, debe ser contextualizada y adaptada a sus necesidades individuales.
Figura 1. Concepción efectiva de la aplicación del constructivismo.
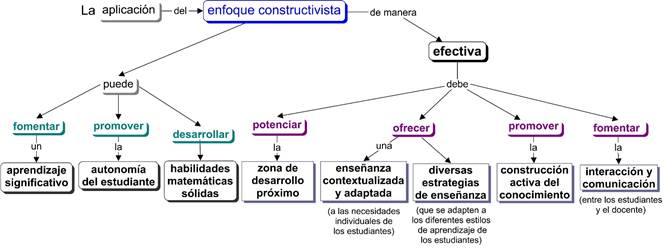
Desde esta concepción, en la práctica de la enseñanza - aprendizaje de la matemática, el conocimiento se ancla mejor en la mente porque no se olvida, debido a que se basa en la voluntad de aprender de los estudiantes y en sus propias experiencias. Desarrolla además habilidades críticas, fomenta la comunicación y la colaboración entre los estudiantes y el profesor, lo que ayuda a desarrollar habilidades interpersonales valiosas para el aprendizaje y la vida en general.
Como parte también de la concepción del enfoque constructivista, para que este sea efectivo, es fundamental que exista un alineamiento constructivo entre los diferentes elementos del proceso de enseñanza – aprendizaje. De esta manera se definirán los objetivos de aprendizaje de manera clara, lo cual permitirá guiar a los estudiantes hacia la construcción del conocimiento deseado, se emplearan los métodos de enseñanza apropiados y se definirá una evaluación coherente.
En relación al alineamiento constructivo, este se basa en el proceso de enseñanza-aprendizaje-evaluación, Biggs (1993) adopta el modelo Propósito-Proceso-Producto (Modelo 3P). Los factores de propósito comprenden los aspectos contextuales (del alumno y de la enseñanza) previos a la acción educativa en un aula (antes de que se produzca el aprendizaje), es el objetivo a lograr. Estos influyen sobre las variables de proceso, las cuales describen la dinámica de enseñanza-aprendizaje que tiene lugar durante la interacción en clase y de la cual resulta la fase de producto, donde se miden los resultados escolares, el desempeño del alumno.
En este sentido, para que se produzca el alineamiento constructivo los componentes Propósito, Proceso y Producto deben funcionar en la enseñanza como un sistema equilibrado. Los elementos integrales del proceso enseñanza, aprendizaje, evaluación (E-A-E) se deben apoyar mutuamente porque forman parte del sistema total, en la figura 2 se representa de forma esquemática éstos componentes.
Figura 2. Componentes del alineamiento constructivo.
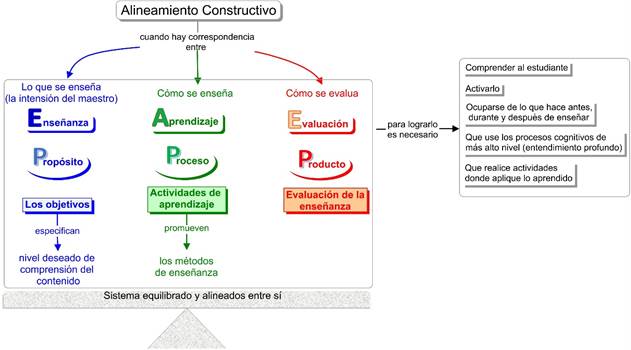
Fuente: Elaboración propia a partir de la concepción del Modelo 3P de Biggs (1993).
En este mismo orden de ideas, la teoría del alineamiento constructivo propuesto por Biggs (2005), para el diseño de la enseñanza se basa en el principio del constructivismo: aprendizaje y alineamiento en la enseñanza. Los componentes que integran dicho modelo son: el currículo que se enseña, los métodos de enseñanza que se utilizan, los procedimientos de evaluación que se usan y los métodos de comunicación de los resultados, el clima que se crea en las interacciones con los estudiantes y el clima institucional, las reglas y procedimientos que se tienen que cumplir.
Según Biggs (2005), para lograr la planeación didáctica de una asignatura se deben considerar los siguientes elementos: los conocimientos previos que tiene el estudiante, sus capacidades, expectativas, habilidades, modos preferentes de aprender, hábitos de trabajo, valores y motivaciones para el estudio; el propósito (objetivo) de la asignatura; los contenidos curriculares a desarrollar; las estrategias o métodos de enseñanza y aprendizaje, donde se tenga en cuenta los niveles de comprensión que se quieren lograr y qué actividades de aprendizaje son las más adecuadas para alcanzar esos niveles; los recursos de aprendizaje; y la evaluación.
Respecto a la evaluación, Biggs (2010, p. 32) planteó que “El principio básico de la buena evaluación consiste en asegurar que esté alineada con el currículo”. Para ello, después que se han definido los objetivos, las tareas y las estrategias de aprendizaje, el docente debe definir la forma en la que lo va a evaluar. La evaluación se debe orientar con los objetivos de manera alineada.
Además, al evaluar los progresos del estudiante desde la concepción constructivista, el proceso se debe convertir en un momento más de formación y aprendizaje, por lo que debe dejar de ser un control y convertirse en mejora. Concebir la evaluación desde esta óptica como lo indica Angelini (2016), incide de manera positiva en su aprendizaje y contribuye a desarrollar el análisis crítico, la autocrítica y su autonomía. Además, se favorece su capacidad de reflexión, pensamiento crítico y aprendizaje para la vida real.
Desde la perspectiva de Hamodi, et al. (2015), el alumnado no aprende con los procesos de calificación, sino con los de evaluación. Para estos autores la evaluación es un proceso basado en recoger información, sea por medio de instrumentos escritos o no; analizar esa información, y emitir un juicio sobre ella para tomar decisiones. La calificación la consideran como la materialización del juicio emitido (tras la recogida de información llevada a cabo) en una nota alfanumérica, que se asigna a un sujeto. Además, consideran las funciones de la evaluación como: formadora, reguladora, pedagógica, comunicadora y ambientadora; y las de la calificación: certificadora, selectiva, comparativa y de control.
En otro orden de ideas, para construir una enseñanza alineada, es necesario especificar el nivel deseado de comprensión del contenido. En tal sentido, Neira, et al. (2016) plantea que se deben seleccionar los verbos adecuados, los que se convertirán en actividades para los estudiantes y, en consecuencia, promoverán los métodos de enseñanza y abordarán las tareas de evaluación.
A medida que los estudiantes aprenden, los resultados de su aprendizaje muestran fases similares de creciente complejidad estructural. Como herramienta para definir la comprensión Biggs (2005), propuso la Taxonomía SOLO (Structure of the Observed Learning Outcome - Estructura del resultado observado del aprendizaje). En ella se definen cinco niveles: preestructural, uniestructural, multiestructural, relacional y abstracto extendido. Puede utilizarse para describir el nivel y la calidad de los aprendizajes para saber en qué nivel concreto se están desenvolviendo los educandos.
Algunas consideraciones en la aplicación del enfoque constructivista en el proceso de enseñanza – aprendiza de la matemática en el bachillerato
Para ayudar a crear un entorno de aprendizaje más significativo y efectivo para los estudiantes de bachillerato, se debe ajustar los contenidos para que sean más relevantes, y significativos. También es necesario enfocarse en la comprensión profunda de los conceptos numéricos y la resolución de problemas, así se vincularía la teoría con la práctica, pues el componente práctico es el que consolida y reafirma los conocimientos y el logro de las habilidades.
En este mismo orden de ideas, se debe colocar al alumno en el centro del proceso de enseñanza-aprendizaje, de modo que sea el principal constructor de su propio conocimiento, esta es una de las principales máximas del modelo de aprendizaje constructivista, el otorgarle un papel protagónico al estudiante. Para lograr esto, entre otras cosas, se podrían diseñar actividades de autoevalución y coevaluación, pues le permitiría producir y no solo reproducir el conocimiento. Respecto a la evaluación, la misma debe ser constante para que el docente pueda saber cuáles son sus progresos y le proporcione retroalimentación formativa oportuna, en la que se ofrezca información correctiva y se aclaren sus dudas sobre qué deben mejorar y qué les hace falta conocer, esto ayuda a enriquecer su aprendizaje y la comprensión de los contenidos.
Desde la concepción constructivista la motivación de los estudiantes es muy importante para asegurar que el aprendizaje sea efectivo. Al aplicar esto a la enseñanza de la matemática, se debe tener en cuenta las perspectivas del alumno sobre la materia y la situación e interacción bajo la cual se producirá el aprendizaje. Es significativo entonces, hacerles comprender la necesidad que tienen de conocer los procedimientos para la aplicación de su vida diaria, y cómo estos conocimientos son la base de otras materias, de esta manera el educando podrá percibir su relevancia y utilidad. De esta manera se elevaría su motivación, compromiso, gusto por aprender y comprender cada utilidad del aprendizaje. Para lograrlo se debe propiciar un ambiente estimulante, nunca bajo amenazas.
Resulta importante también ocuparse de lo que el alumno hace ante, durante y después de enseñar, es decir, del producto o el resultado del aprendizaje de la enseñanza (principio del tercer nivel de enseñanza). Además, es necesario lograr que use los procesos cognitivos de más alto nivel, en el que adquiera un entendimiento profundo.
Es significativo para la obtención de resultados satisfactorios en el aprendizaje de los estudiantes al aplicar el enfoque constructivista, que el docente cumpla con el rol que le corresponde. En este sentido, debe ser capaz de proporcionar a los alumnos las estrategias necesarias para promover un aprendizaje interactivo y dinámico. Debe ser tutor, supervisor o guía del proceso, mentor, animador, mediador, proveedor de recursos, innovador y creativo. También, tiene que ser capaz de diseñar materiales de aprendizaje para el estudio de los contenidos a un nivel básico para que todos puedan comprenderlo con facilidad y les sirva de guía de orientación bajo la primicia de explica y aplica. Resulta preciso además, que les brinde asistencia a lo largo del proceso, en el que realice un trabajo diferenciado con los de necesidades especiales.
Integración de las tecnologías en el proceso de enseñanza - aprendizaje de la matemática
Cuando los estudiantes construyen su propio conocimiento a través de experiencias significativas como se concibe en el enfoque constructivista, el uso de herramientas tecnológicas como simulaciones, aplicaciones interactivas y plataformas de aprendizaje en línea, les permite explorar conceptos matemáticos de manera dinámica y visual. Esto facilita la comprensión profunda de las ideas claves y fomenta la participación activa en la resolución de problemas. Además, permiten a los docentes crear entornos de aprendizaje personalizados, adaptar los contenidos a las necesidades individuales de los estudiantes y brindar retroalimentación oportuna.
En este sentido, Delgado y González (2023), al determinar el impacto del modelo pedagógico constructivista en ambientes virtuales de aprendizaje, evidenció que ante una adecuada integración de contenidos y experticia de los docentes en el manejo de las herramientas de gestión de contenidos, se mejora de manera significativa el éxito en el aprendizaje y se logra que este sea más significativo y con mayor autonomía por parte de los alumnos. Además, permiten al educando adquirir conocimientos de forma dinámica, desarrollar habilidades como el autoaprendizaje y emprendimiento; así como realizar trabajo colaborativo.
Parra et al. (2022) por su parte, considera que incluir las tecnologías en los procesos educativos por sí sola no constituye un factor determinante de efectividad, para lo cual plantea la teoría constructivista como complemento. Esto lo traduce entonces en beneficios de un verdadero aprendizaje significativo que perdura en el tiempo y da origen a nuevos conocimientos, así como también en el desarrollo de habilidades cognitivas de orden superior. Aunque, señala que el acceso a los recursos tecnológicos puede convertirse en una limitante.
En la integración de las tecnologías en el proceso de enseñanza - aprendizaje de la matemática, debe tenerse en cuenta como describe, Padilla et al. (2014), que se pone en perspectiva una serie de cambios curriculares, pedagógicos, didácticos y evaluativos. En tal sentido, existen diversos recursos tecnológicos que permiten fortalecer el aprendizaje a través de la organización del conocimiento, con la integración de diferentes actividades, que provocan un aprendizaje significativo al estudiante y le otorgan un papel activo para generar su propio aprendizaje a través de referentes constructivistas.
En los momentos actuales, incorporar al proceso educativo las TIC también contribuye a elevar la motivación y la independencia de los educandos en la solución de las tareas de aprendizaje, diseñar diferentes materiales para facilitar la enseñanza con distintos estilos de aprendizaje, optimizar el tiempo presencial, promover la retroalimentación constante y flexibilizar la forma de entrega del conocimiento.
En el contexto del proceso formativo en matemática, Barrios y Delgado (2022) defiende el criterio de que el empleo de las tecnologías tienen un efecto satisfactorio si se usan de forman adecuada. Poyato (2021) por su parte, manifiesta que el empleo de metodologías activas y las herramientas digitales resultan motivadoras, fomentan el aprendizaje, aumentan los tiempos de concentración y de trabajo, lo que posibilita un acercamiento autónomo a los contenidos de esta disciplina.
Entre tanto, Vivanco et al. (2023), describieron como falencia que existe en el proceso de incorporación de las TIC al proceso de enseñanza - aprendizaje de la matemática en estudiante de bachillerato, el escaso conocimiento que tienen algunos docentes, lo cual limita que se le pueda sacar el mayor provecho posible o que no se usen. De ahí que reconocen la necesidad de que estos adquieran las competencias mediante una actualización y capacitación constante, de modo que no solo sean capaces de emplearlas de forma correcta, sino además que puedan seleccionar las más adecuadas y planificar estrategias metodológicas efectivas de integración. Estos autores presentaron también una guía prácticas sobre el uso de las herramientas GeoGebra y PhET.
Otra de las herramientas tecnologías factibles para emplearse bajo el enfoque constructivista, lo constituyen los entornos virtuales de aprendizaje, los cuales permiten complementar la educación presencial con la virtual. Bajo este marco de trabajo en el proceso de enseñanza – aprendizaje de la matemática, se podrían diseñar actividades como wikis, glosario, talleres y foros. De esta manera se promovería la interacción y colaboración entre ellos y a su vez con el docente. Cada actividad debe estar diseñada de modo que cause en los educandos la discusión, el análisis, la adquisición y la transmisión del conocimiento.
Experiencias en la aplicación del enfoque constructivista y el uso de las tecnologías en el proceso de enseñanza - aprendizaje de la matemática
Varias son las experiencias de la aplicación del enfoque constructivista y el uso de las TIC. En tal caso se puede citar a Mendoza y García (2022), quienes al evaluar la estrategia didáctica constructivista con enfoque inclusivo para el aprendizaje de matemática de tercero de bachillerato en los estudiantes con necesidades educativas especiales asociadas a la discapacidad en una unidad educativa en Ecuador, se pudo constatar su efectividad al desarrollar en los alumnos, hábitos de estudio, autoformación e independencia educativa. La propuesta se basa en la incorporación en su práctica curricular el empleo de videos de Youtube, plataformas informáticas y otros materiales tecnológicos. Armas et al. (2023), también fundamentó una propuesta basada en el uso de las TIC y el constructivismo como modelo didáctico, centrado en lograr un aprendizaje significativo y cooperativo; así como, la implicación del alumnado en su propio proceso de aprendizaje y que despierte el interés por la asignatura.
Entre tanto, Amores y Ramos (2020), presentaron resultados de un análisis basado en la pedagogía constructivista en el proceso de enseñanza-aprendizaje en asignaturas esenciales entre la que se encuentra matemática, en una unidad educativa de Educación General Básica en Cotopaxi, Ecuador. Estos autores detectaron distintos problemas de aprendizaje como distracción, aburrimiento, falta de interés, entre otros, los cuales dificultaban el aprendizaje. Se determinó que la situación estuvo dada porque el profesorado, en teoría, conoce los conceptos de la pedagogía constructivista, sin embargo, al momento de trasladarlo al aula, no lo aplican. Esto pone en evidencia que las falencias detectadas en el proceso educativo no son precisamente por limitaciones del modelo constructivista, sino más bien por no emplearlo o hacerlo de manera inadecuada.
En relación al empleo de las TIC como herramienta para mejorar el rendimiento académico de los estudiantes en matemática, se conoce la experiencia de Arteaga (2023), quien realizó un estudio con alumnos de secundaria en Chachapoyas, Perú. Esta autora pudo evidenciar una relación moderada entre las TIC y el rendimiento académico en dicha materia y validar un efecto positivo cuando existe un uso racional y eficaz de las TIC. En consonancia con esto se encuentra el estudio realizado por Semanate y Robayo (2021), quienes propusieron una estrategia didáctica basada en el uso de las TIC para mejorar el desempeño académico en matemática en los alumnos de segundo año de bachillerato de la Unidad Educativa Vicente León, en Ecuador. Los autores constataron que la propuesta beneficia la apropiación de los conocimientos, la capacidad de razonamiento crítico, la curiosidad intelectual, el mejoramiento cognitivo y la apropiación de contenidos a través de la teoría y la práctica.
Otra experiencia en el empleo de las TIC la presentó Sánchez y Hernández (2024), al mostrar resultados satisfactorios con el uso de Mobile Learning a través de la aplicación GeoGebra y enfoque STEAM (Ciencia, Tecnología Ingeniería, Arte y Matemáticas), en grupos de matemáticas de bachillerato. De igual manera Cañizares y Reyes (2023), también obtuvieron resultados satisfactorios con el uso de este software en alumnos de primero, segundo y tercero de bachillerato de la Unidad Educativa El Pan, de la provincia del Azuay, cantón El Pan, Ecuador. Desde su apreciación, son muchas las ventajas que posee para crear clases más dinámicas y activas.
En Ecuador también, Moreira y Rivadeneira (2023) propusieron estrategias educativas digital para fortalecer el proceso de enseñanza de la asignatura de matemática en la Unidad Educativa Raffaello Santi de Portoviejo, provincia de Manabí. La propuesta consistió en la implementación de un ambiente de aprendizaje basado en la plataforma CANVAS con apoyo del enfoque constructivista social tecnológico. Muentes y Triviño (2024) por su parte, presentaron actividades didácticas con la utilización de digital Math Cilenia para mejorar el aprendizaje de matemática en los alumnos con discalculia del nivel de bachillerato técnico y General Unificado de la Unidad Educativa Picoazá. En el caso de Rosero et al. (2023), el estudio se realizó con alumnos de las unidades educativas en el Cantón Quevedo, Provincia de Los Ríos, en el que se pudo evidenciar que la aplicación de las TIC en el aprendizaje de los educandos en esta disciplina favorece la existencia de un aprendizaje más significativo, una mejor asimilación de los contenidos, de una manera dinámica, novedosa y comprensible, con resultados satisfactorios.
CONCLUSIONES
Luego de analizarse los elementos claves de la teoría del aprendizaje constructivista, teniéndose en cuenta el postulado del alineamiento constructivo; así como, las potencialidades de la incorporación de las herramientas tecnológicas a los procesos educativos desde esta concepción, lo cual se acreditó en los resultados alcanzados por diversos autores que lo aplicaron, se evidencia que se favorece el proceso de enseñanza – aprendizaje de la matemática en el bachillerato.
El proceso educativo de esta disciplina, se favorecería con el logro de un aprendizaje activo, significativo y por descubrimiento autónomo en los estudiantes, en el que le permitiría comprender, aprender, recordar y aplicar mejor los conceptos, para resolver problemas matemáticos. Además, se elevaría la motivación por el estudio y se podría lograr un entendimiento profundo en los educandos.
REFERENCIAS
Amores, J. L. y Ramos, G. (2020). Limitaciones del modelo constructivista en la enseñanza-aprendizaje de la Unidad Educativa Salcedo, Ecuador. Revista Educación, 45(1), 36-51. https://doi.org/10.15517/revedu.v45i1.41009
Angelini, M. L. (2016). Análisis y estrategias en la aplicación de la evaluación formativa y compartida en magisterio. Revista Latinoamericana de Estudios Educativos, XLVI(1), 51-78. http://www.redalyc.org/articulo.oa?id=27044739003
Armas, T. R., Hernández, V. M. y Mato, M. del C. (2023). Propuesta didáctica de Matemáticas de 3o de ESO: aplicaciones tecnológicas del saber algebraico. FPIEM: Formación del Profesorado e Investigación en Educación Matemática, 15, 29-68. https://dialnet.unirioja.es/servlet/articulo?codigo=9504890https://dialnet.unirioja.es/servlet/articulo?codigo=9504890
Arteaga, M. (2023). TICs en el rendimiento académico de matemática en estudiantes de secundaria Chachapoyas, Perú. Educación y Vida Sostenible, 1(3), 89-100. https://doi.org/10.57175/evsos.v1i3.37
Barrios, L. M. y Delgado, M. (2022). Efectos de los recursos tecnológicos en el aprendizaje de las matemáticas. Revista Digital Matemática, Educación e Internet, 22(1). https://revistas.tec.ac.cr/index.php/matematica/article/view/5731
Biggs, J. B. (1993). From Theory to practice: A cognitive systems approach. Higher Education Research and Devpmenelot, 12, 73-86. https://doi.org/10.1080/0729436930120107
Biggs, J. B. (2005). Calidad del aprendizaje universitario. Madrid: Nancea de Ediciones (Segunda). https://barajasvictor.wordpress.com/wp-content/uploads/2014/05/libro-j-biggs.pdf
Biggs, J. B. (2010). Calidad del Aprendizaje Universitario (Narcea, SEP-ANUIES).
Cañizares, M. V. y Reyes, D. B. (2023). Contribuciones de las TIC’s para el desarrollo del pensamiento con estudiantes de BGU. Un aporte desde las matemáticas. LATAM Revista Latinoamericana de Ciencias Sociales y Humanidades, 4(2), 3750-3771. https://doi.org/10.56712/latam.v4i2.868
Contreras, D. (2021). El constructivismo para mí y el constructivismo en sí. Revista Observatorio de las Ciencias Sociales en Iberoamérica, 2(8), 1-11. https://www.eumed.net/uploads/articulos/3b64b6cc6ee238ba31b8b900458ec22c.pdf
Delgado, D. y González, A. (2023). Eficacia del modelo pedagógico constructivista dentro ambientes virtuales de aprendizaje. RES NON VERBA, 13(1), 1-14. https://doi.org/10.21855/resnonverba.v13i1.679
Esquivel, R. A. (2023). Actitudes hacia las matemáticas en estudiantes de secundaria: Presentación y descripción de resultados. MENDIVE, 21(4). https://mendive.upr.edu.cu/index.php/MendiveUPR/article/view/3231
Gómez, R. O. y Pérez, G. (2023). Las metodologías activas y su influencia en rendimiento académico de estudiantes de bachillerato. MQRInvestigar, 7(1), 3048-3069. https://doi.org/10.56048/MQR20225.7.1.2023.3048-3069
Gutiérrez, R. (1987). Psicología y aprendizaje de las ciencias: El modelo de Ausubel. Enseñanza de las Ciencias, 5(2), 118-128. https://www.raco.cat/index.php/Ensenanza/article/download/50960/92902
Hamodi, C., López, V. M. y López, A. T. (2015). Medios, técnicas e instrumentos de evaluación formativa y compartida del aprendizaje en educación superior. Perfiles educativos, 37(147), 146-161. https://perfileseducativos.unam.mx/iisue_pe/index.php/perfiles/article/view/47271/42553
Hernández, C. R. (2015). Hacia una comprobación experimental de la zona de desarrollo próximo de Vigotsky. CIENCIA ergo-sum, 22(2), 167-171. https://www.redalyc.org/pdf/104/10439327009.pdf
Li, Y. y Schoenfeld, A. H. (2019). Problematizing teaching and learning mathematics as “given” in STEM education. International Journal of STEM Education, 6(1), 44. https://doi.org/10.1186/s40594-019-0197-9
Martínez, X., Pons, J., Turon, F., Coma, M., Barbu, L. G. y Bugeda, G. (2023). Multi-Objective Multi-Scale Optimization of Composite Structures, Application to an Aircraft Overhead Locker Made with Bio-Composites. Mathematics, 11(1). https://doi.org/10.3390/math11010165
Mendoza, Y. P. y García, R. (2022). Estrategia didáctica constructivista con enfoque inclusivo para el aprendizaje de matemáticas en los estudiantes con necesidades educativas especiales. Revista Alcance, 6(2). https://doi.org/10.47230/ra.v2i6.45
Miranda, Y. R. (2020). Praxis educativa constructivista como generadora de aprendizaje significativo en el área de Matemática. CIENCIAMATRIA, 6(1), 141-163. https://doi.org/10.35381/cm.v6i1.299
Miranda, Y. R. (2022). Aprendizaje significativo desde la praxis educativa constructivista. Revista Arbitrada Interdisciplinaria Koinonía, 7(13), 79-91. http://dx.doi.org/10.35381/r.k.v7i13.1643
Moreira, A. P. y Rivadeneira, F. (2023). Estrategia educativa digital para la enseñanza de la asignatura de matemática. CIENCIAMATRIA, 9(1), 1030-1051. https://doi.org/10.35381/cm.v9i1.1115
Muentes, R. A. y Triviño, J. R. (2024). Uso del recurso digital math cilenia en el aprendizaje de las matemáticas en estudiantes con discalculia del bachillerato. MQRInvestigar, 8(1), 4359-4383. https://doi.org/10.56048/MQR20225.8.1.2024.4359-4383
Navarro, I., González, C., López, B. y Contreras, A. (2019). Aprendizaje cooperativo basado en proyectos y entornos virtuales para la formación de futuros maestros. Educar, 55(2), 1-23. https://raco.cat/index.php/Educar/article/view/v55-n2-navarro-gonzalez-lopez-contreras
Neira, L., Nemeguen, W. y Soler, M. (2016). Alineamiento constructivo y cambio conceptual para la enseñanza de los estados de agregación de la materia. Revista Tecné, Episteme y Didaxis: TED, Extraordinario, 307-315. https://revistas.upn.edu.coindex.php/TED/article/view/4544
Padilla, J. E., Vega, P. L. y Rincón, D. A. (2014). Tendencias y dificultades para el uso de las TIC en educación superior. Entramado, 10(1), 272-295. http://www.redalyc.org/articulo.oa?id=265431574018
Parra, D. S., Chiluiza, W. P. y Castillo, D. A. (2022). Inclusión tecnológica en época de pandemia: Una mirada al constructivismo como fundamento teórico. Revista Tecnológica-Educativa Docentes 2.0, 13(2), 16-25. https://doi.org/10.37843/rted.v13i2.288
Parrat, S. (2012). Esencia y trascendencia de la obra de Jean Piaget (1896-1980). Persona, 15, 213-224. http://www.redalyc.org/articulo.oa?id=147125259012
Piaget, J. (1949). La pedagogía moderna. Lausana, 152(65).
Poyato, F. J. (2021). Relación entre motivación por las matemáticas y aprendizaje activo a través de herramientas digitales. Épsilon - Revista de Educación Matemática, 107, 59-65. https://www.saemthales.es/epsilon_d9/sites/default/files/2023-02/epsilon107_5.pdf
Raynaudo, G. y Peralta, O. (2017). Cambio conceptual: Una mirada desde las teorías de Piaget y Vygotsky. Liberabit: Revista de Psicología, 23(1), 137-148. https://doi.org/10.24265/liberabit.2017.v23n1.10
Rosero, J. A., Topa, C. P., Mestanza, P. A. y Ruiz, L. V. (2023). El uso tecnológico para la enseñanza-aprendizaje de las Matemáticas en los estudiantes de las unidades educativas. Maestro y Sociedad, 20(4), 1042-1050. https://maestroysociedad.uo.edu.cu/index.php/MyS/article/view/6276
Saldarriaga, P. J., Bravo, G. del R. y Loor, M. R. (2016). La teoría constructivista de Jean Piaget y su significación para la pedagogía contemporánea. Dominio de las ciencias, 2(esp.), 127-137. https://dialnet.unirioja.es/servlet/articulo?codigo=5802932
Sánchez, C. y Hernández, F. T. (2024). Del sistema tradicional hacia uno significativo, el reto del docente en matemáticas. Revista Varela, 24(68), 155-164. https://doi.org/10.5281/zenodo.11090126
Semanate, D. E. y Robayo, D. J. (2021). Estrategia didáctica basada en TIC para mejorar el desempeño académico en el área de Matemática. EPISTEME KOINONIA, 4(8), 388-412. https://doi.org/10.35381/e.k.v4i8.1384
Vivanco, J., Tocto, J., Mogrovejo, J., León, F. y Vivanco, C. (2023). Herramientas Web 2.0 en la enseñanza aprendizaje de matemáticas. Una revisión bibliográfica. LATAM Revista Latinoamericana de Ciencias Sociales y Humanidades, 4(2), 878-901. https://doi.org/10.56712/latam.v4i2.657
Walter, L., Gallegos, A. y Huerta, A. O. (2014). Aprendizaje por descubrimiento vs. Aprendizaje significativo: Un experimento en el curso de historia de la psicología. Boletim-Academia Paulista de Psicologia, 34(87), 455-471. https://www.redalyc.org/pdf/946/94632922010.pdf