Vol. 4 | No. 8 | Agosto 2024 - enero 2025 | ISSN: 3006-1385 | ISSN-L: 3006-1385 | Pág. 22 - 35

Red neuronal para predecir el rendimiento académico

Neural network to predict academic performance

Maya René Choque Aguilar

maya.choque@uab.edu.bo

https://orcid.org/0000-0001-7123-7302

Universidad Adventista de Bolivia, Cochabamba, Bolivia

Artículo recibido 28 de mayo de 2024 / Arbitrado 06 de junio de 2024 / Aceptado 03 de julio 2024 / Publicado 30 de agosto de 2024

http://doi.org/10.62319/simonrodriguez.v.4i8.31

RESUMEN

Este estudio presenta un modelo diseñado para predecir el rendimiento académico utilizando redes neuronales. Se enmarca en un enfoque cuantitativo y se categoriza como un estudio correlacional multivariado. La investigación se basa en una base de datos proveniente de una institución educativa, disponible en el repositorio de datos de la Universidad de California, Irvine. Se eligió R como el lenguaje de programación, con RStudio como entorno de desarrollo. Se adoptó la metodología CRISP-DM para llevar a cabo el análisis de datos. La construcción de la red neuronal se realizó utilizando el paquete nnet, disponible en el Comprehensive R Archive Network (CRAN). El modelo de red neuronal se aplicó a los datos recopilados de 649 estudiantes, y su capacidad predictiva se evaluó exhaustivamente. Tras compararlo con un modelo de regresión lineal múltiple, se observó que el modelo de red neuronal logró una efectividad del 87% en la predicción del rendimiento académico, evidenciando su idoneidad para este propósito.

Palabras clave: redes neuronales, predicción, rendimiento académico

ABSTRACT

This study presents a model designed to predict academic performance using neural networks. It is framed within a quantitative approach and is categorized as a multivariate correlational study. The research is based on a database from an educational institution, available in the data repository of the University of California, Irvine. R was chosen as the programming language, with RStudio as the development environment. The CRISP-DM methodology was adopted to carry out the data analysis. The construction of the neural network was carried out using the nnet package, available in the Comprehensive R Archive Network (CRAN). The neural network model was applied to data collected from 649 students, and its predictive ability was comprehensively evaluated. After comparing it with a multiple linear regression model, it was observed that the neural network model achieved an effectiveness of 87% in predicting academic performance, evidencing its suitability for this purpose.

Kewords: neural networks, prediction, academic performance

INTRODUCCIÓN

La problemática de la deserción estudiantil es una preocupación recurrente en las instituciones de educación superior, particularmente destacada en las carreras de ingeniería. Esta problemática puede atribuirse a una variedad de factores, como limitaciones financieras, conflictos familiares, carencias en la preparación en ciencias exactas, y desempeño académico insuficiente, entre otros.

La capacidad de anticipar la probabilidad de abandono de estudios por parte de un estudiante constituye un recurso invaluable para los profesores y administradores educativos. Dicha anticipación proporcionaría información crucial para la planificación y ejecución de programas destinados a ofrecer apoyo a estos estudiantes en riesgo. De este modo, se podría mitigar la deserción estudiantil, garantizando así la prestación de un servicio educativo óptimo y promoviendo la excelencia académica en la institución educativa.

En este estudio, se emplearon redes neuronales como herramienta para abordar uno de los factores contribuyentes a la deserción estudiantil: el rendimiento académico. Flóres López y Fernandez (2008) define las redes neuronales como modelos de cálculo caracterizados por algoritmos altamente eficientes que operan de manera masivamente paralela, facilitando tareas como el aprendizaje de patrones, la clasificación y la optimización. Según Caicedo Bravo y López Sotelo (2009), el propósito de las redes neuronales es emular el funcionamiento de las neuronas del cerebro humano, una iniciativa que se remonta a hace mucho tiempo atrás, pero que ha experimentado un verdadero avance gracias a la disponibilidad de computadoras con capacidades de procesamiento superiores.

Por otro lado, Pawlus y Devine (2020) destaca que, a pesar de las diferencias significativas en el proceso de aprendizaje entre un cerebro humano y una red neuronal, estas últimas son capaces de resolver problemas extremadamente complejos debido a su estructura similar. Además, Heaton (2012) señala que las redes neuronales abarcan diversas áreas de las matemáticas. Aquellas utilizadas para clasificación, regresión y agrupamiento requieren conocimientos de estadística, mientras que aquellas que emplean algoritmos como el backpropagation necesitan comprensión en cálculo.

En este contexto, Graupe (2013) resalta el potencial de las redes neuronales para resolver problemas relacionados con la predicción, reconocimiento, diagnóstico, filtración y control. Sin embargo, el autor menciona que estas no son apropiadas para resolver situaciones deterministas bien definidas. Matich (2001) hace hincapié en la fortaleza de las redes neuronales en el reconocimiento de patrones, lo que se traduce en diversas aplicaciones prácticas, como la predicción del tiempo, la evaluación de riesgos crediticios, la optimización de horarios en líneas de vuelo, el control del tráfico, el reconocimiento de imágenes, entre otros campos como la visión artificial y el diagnóstico médico basado en síntomas.

La versatilidad de las redes neuronales se manifiesta en su aplicación en los tres principales grupos de problemas de la Inteligencia Artificial: aprendizaje supervisado, aprendizaje no supervisado y aprendizaje por refuerzo. Esta diversidad de usos ofrece un vasto campo de posibilidades en diversos sectores, incluida la educación.

La incursión de la Inteligencia Artificial en el ámbito educativo es una tendencia reconocida y promovida por la UNESCO. Según Buckingham (2012), estas técnicas tienen el potencial de revolucionar la investigación educativa, convirtiéndola en una disciplina orientada a los datos y permitiendo que las instituciones educativas adopten una cultura de toma de decisiones fundamentada en la evidencia.

Ocaña Fernandez et al. (2019) destaca que el aprovechamiento de la Inteligencia Artificial promete mejoras cualitativas sin precedentes, siendo una de ellas la capacidad de ofrecer a cada estudiante una personalización precisa de su proceso de aprendizaje. Además, Sanchez Vila y Lama Penin (2007) señala diversas aplicaciones de la Inteligencia Artificial en educación, como tutores inteligentes, sistemas de evaluación automática, aprendizaje colaborativo asistido por computadora y aprendizaje basado en juegos.

Por otro lado, Macías Moles (2021) subraya que, si bien la Inteligencia Artificial ya ha comenzado a utilizarse en el ámbito educativo, aún enfrenta desafíos significativos para integrarse plenamente en las aulas y alcanzar su máximo potencial. Este reconocimiento de los avances y desafíos pendientes ilustra la evolución y el camino futuro de la Inteligencia Artificial en el contexto educativo.

El propósito principal de este estudio es desarrollar una red neuronal capaz de predecir el rendimiento académico de los estudiantes. En este contexto, se busca identificar variables clave que puedan influir en el éxito o fracaso del rendimiento académico. Específicamente, el modelo tiene como objetivo anticipar el rendimiento académico de un estudiante individual (variable de respuesta numérica) a partir de una serie de variables adicionales (variables explicativas numéricas y/o categóricas).

En consecuencia, algunos de los objetivos secundarios incluyen:

• Obtener una fuente de datos adecuada para llevar a cabo el análisis.
• Identificar las variables que servirán como entrada para la red neuronal.
• Determinar la estructura apropiada de la red neuronal y proceder con su construcción.
• Validar los resultados generados por la red neuronal, asegurando su fiabilidad y precisión.

Estos objetivos secundarios están diseñados para respaldar el logro del objetivo principal, contribuyendo a la construcción y validación de un modelo predictivo efectivo para el rendimiento académico estudiantil.

Se han realizado varias investigaciones relevantes sobre el rendimiento académico y el uso de redes neuronales en diferentes contextos educativos.

Longoni et al. (2010) llevó a cabo un análisis del rendimiento académico de los estudiantes que ingresaron a la Facultad de Ciencias Exactas, Naturales y Agrimensura de la Universidad Nacional de Nordeste (FCENA - UNNE) en Corrientes, Argentina. Utilizó redes neuronales tipo Perceptrón Multicapa (PM) y de base radial (FBR), obteniendo porcentajes de clasificación correcta de 78.2%, 70.7%, 75.7% y 68.6%, respectivamente.

Zambrano Matamala et al. (2011) realizó un estudio utilizando una arquitectura de Data Warehouse (DW) para analizar el desempeño académico. Aunque un DW no es capaz de realizar estudios predictivos por sí solo, se utilizó como entrada para la red neuronal. Este estudio, basado en datos de la Universidad de Atacama, destacó la eficacia de las redes neuronales en la predicción del rendimiento académico, aunque no se proporcionaron los porcentajes de clasificación correcta.

Salgado Reyes et al. (2018) investigó el rendimiento académico de 300 estudiantes en la plataforma Moodle de la Universidad Central del Ecuador utilizando redes neuronales. El análisis se centró en materias específicas como Programación I, Estructura de Datos, Programación Distribuida y Aplicaciones de Minería de Datos, con un promedio de precisión del 75.28%.

Incio et al. (2021) reportó una investigación realizada con estudiantes de Ingeniería Civil en la Universidad UNIFSLB de Perú, utilizando datos históricos y software como MATLAB, junto con algoritmos como Scaled Conjugate Gradient y Levenberg-Marquardt para construir la red neuronal. Los porcentajes de predicción obtenidos fueron del 70% y 86%.

Por último, Porcel et al. (2009) estableció una relación entre el rendimiento académico de los estudiantes de primer año y su nivel de conocimientos previos. Utilizó métodos como la regresión logística, árboles de decisión y redes neuronales, aunque no se proporcionaron los porcentajes de precisión de las redes neuronales utilizadas. Estas investigaciones proporcionan una perspectiva amplia sobre el uso de redes neuronales en la predicción del rendimiento académico y su relación con diferentes variables.

MÉTODO

El enfoque de esta investigación es cuantitativo, lo que implica la recopilación y el análisis de datos numéricos para comprender y explicar fenómenos sociales o naturales. Además, se clasifica como un estudio correlacional multivariado, lo que significa que se busca establecer la relación entre múltiples variables sin necesariamente inferir causalidad. Este tipo de enfoque permite examinar cómo se relacionan entre sí varias variables de interés, como el rendimiento académico de los estudiantes y diferentes factores que pueden influir en él, sin asumir que una variable causa directamente cambios en otra.

Para esta investigación, se empleó una base de datos proveniente de una institución educativa en Portugal, la cual se encuentra alojada en el repositorio de datos de la Universidad de California, Irvine. Una de las ventajas destacadas de este conjunto de datos radica en su amplitud, ya que no solo comprende información académica, sino que también abarca aspectos demográficos y sociales relevantes, como el nivel educativo de la madre.

A continuación, se presenta un resumen de los campos que conforman esta base de datos:

- school: nombre de la institución del estudiante.

- sex: género del estudiante.

- age: edad del estudiante.

- address: tipo de dirección del hogar del estudiante.

- famsize: tamaño de la familia del estudiante.

- Pstatus: estado de cohabitación con los padres.

- Medu: nivel educativo de la madre.

- Fedu: nivel educativo del padre.

- Mjob: ocupación de la madre.

- Fjob: ocupación del padre.

- reason: motivo de elección de la institución.

- guardian: tutor del estudiante.

- traveltime: tiempo de viaje desde el hogar hasta la institución.

- studytime: tiempo de estudio semanal.

- failures: número de clases reprobadas anteriormente.

- schoolsup: apoyo educativo fuera de la institución.

- famsup: apoyo educativo por parte de la familia.

- paid: clases extras pagadas dentro del tema de la clase.

- activities: participación en actividades extracurriculares.

- nursery: asistencia a guardería.

- higher: aspiración a educación superior.

- internet: acceso a internet en el hogar.

- romantic: estado de relaciones románticas.

- famrel: calidad de la relación familiar.

- freetime: tiempo libre después de clases.

- goout: frecuencia de salidas con amigos.

- Dalc: consumo de alcohol durante los días de semana.

- Walc: consumo de alcohol durante los fines de semana.

- health: estado de salud actual.

- absences: número de ausencias en la institución.

- G1: calificación de matemáticas en el primer período.

- G2: calificación de matemáticas en el segundo período.

- G3: calificación final.

El análisis de datos en esta investigación se llevó a cabo utilizando el lenguaje de programación R. Según Gardener (2012), R está emergiendo rápidamente como la herramienta estándar de facto entre los profesionales estadísticos. Se destaca por ser gratuito, de código abierto, poderoso y flexible. Además, ofrece un entorno de herramientas amplio y flexible bajo la licencia GNU GPL, respaldado por la Fundación para la Computación Estadística (FSC).

Además de R, se utilizó RStudio como Entorno de Desarrollo Integrado (IDE). Este software ofrece numerosos beneficios, incluyendo un conjunto de herramientas diseñadas para aumentar la productividad en el análisis de datos. Gandrud (2015) menciona que, aunque R posee todas las capacidades necesarias para recopilar y analizar datos, RStudio simplifica las tareas requeridas para llevar a cabo una investigación reproducible al gestionar de manera eficiente paquetes como knitr y markdown.

Desde el punto de vista estadístico, el análisis se centró en el uso de redes neuronales como método predictivo. Una vez obtenidos los resultados de la predicción utilizando redes neuronales, se llevó a cabo una comparación con un análisis de regresión lineal múltiple. Esta comparación permitió evaluar la eficacia relativa de ambos enfoques en la predicción del rendimiento académico de los estudiantes.

Para el proceso de análisis de datos, se optó por utilizar la metodología CRISP-DM (Cross-Industry Standard Process for Data Mining). Según Shafique y Qaiser (2014), en la actualidad existen tres modelos ampliamente utilizados para el análisis de datos: KDD (Knowledge Discovery in Databases), CRISP-DM y SEMMA (Sample, Explore, Modify, Model, Assess). El autor destaca que la metodología CRISP-DM se encuentra en un punto intermedio, ya que cuenta con menos fases que KDD pero es más completa que SEMMA.

Dada esta consideración, se seleccionó la metodología CRISP-DM como el marco de trabajo adecuado para guiar el proceso de análisis de datos en esta investigación. Esta metodología proporciona una estructura sistemática y bien definida para llevar a cabo todas las etapas del proceso de minería de datos, desde la comprensión del negocio y los datos hasta la evaluación de los resultados del modelo.

RESULTADOS

En primera instancia, se realizó una división de los datos de la siguiente manera: 70% para entrenamiento, 15% para validación y 15% para las pruebas. El código utilizado para este fin, fue el siguiente:

Figura 1. Código fuente de partición de los datos

En esencia, una red neuronal consta de tres capas principales: la capa de entrada, las capas ocultas y la capa de salida. Un modelo convencional de esta arquitectura puede visualizarse mediante la siguiente representación gráfica:

Figura 2. Modelo tradición de una red neuronal

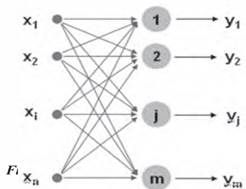
Fuente: Caicedo Bravo y López Sotelo (2009).

Para abordar este problema, la capa de salida se configura con un solo nodo, que refleja la calificación final y sirve como indicador de rendimiento académico, denotando si el estudiante reprueba o no la materia. Para determinar las variables de la capa de entrada, inicialmente se llevó a cabo un análisis de correlación. Posteriormente, se descartaron las variables con valores de p superiores a 0.05, reteniendo únicamente aquellas que poseen una significancia mayor en la capacidad predictiva.

Para la realización del análisis de correlación multivariable se empleó el método de Pearson. El código utilizado para esta tarea se presenta a continuación:

Figura 3. Código fuente para aplicar el método de Pearson

El resultado fue el siguiente:

Figura 4. Análisis de correlación multivariable

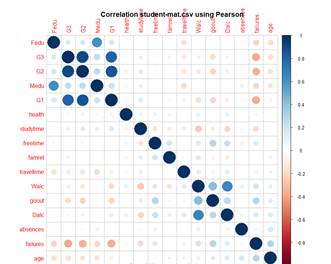
El gráfico revela una correlación significativa entre las calificaciones de las evaluaciones iniciales (G1 y G2) y la calificación final (G3). Esta observación sugiere qué nodos podrían integrar la capa de entrada, proporcionando una comprensión inicial de las variables relevantes para el modelo.

A continuación, se elaboró un modelo inicial de regresión lineal múltiple con el objetivo de identificar los nodos para la capa de entrada. Se consideraron todas las variables pertinentes en el análisis. A continuación, se presenta el código utilizado para esta tarea:

Figura 5. Código fuente de regresión lineal

A continuación, en la siguiente figura se puede ver el resultado de este análisis:

Figura 6. Análisis exploratorio de regresión lineal múltiple

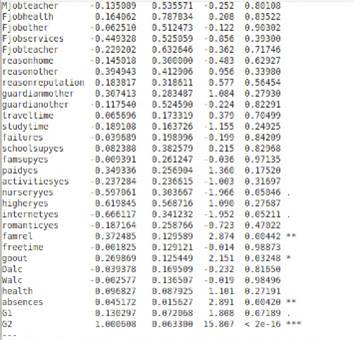
A continuación, se llevó a cabo la optimización del modelo mediante la estrategia de eliminación retroactiva basada en el valor-p y el valor ajustado del coeficiente de determinación R2. El objetivo consistió en obtener un conjunto de nodos para la capa de entrada que maximizara el valor ajustado de R2.

En este sentido, previamente se eliminaron los predictores con un alto valor-p, que incluyen: "sexM", "age", "addressU", "famsizeLE3", "PstatusT", "Medu", "Pedu", "Mjobhealth", "Mjobother", "Mjobservices", "Mjobteacher", "Fjobhealth", "Fjobother", "Fjobservices", "Fjobteacher", "reasonhome", "reasonother", "reasonreputation", "guardianmother", "guardiananother", "traveltime", "studytime", "failures", "schoolsupyes", "famsupyes", "paidyes", "activitiesyes", "nurseryyes", "higheryes", "internetyes", "romanticyes", "freetime", "goout", "Dalc", "health", "G1". Por otro lado, se conservaron los predictores con un valor-p menor, que son: "famrel", "absences", "G2".

El resultado obtenido tras este proceso fue el siguiente:

Figura 7. Análisis de regresión lineal múltiple.

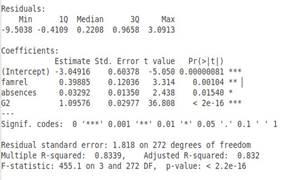
Como se ha observado, el valor ajustado de 𝑅2 es de 0.83, lo que indica un alto grado de precisión en la predicción de las variables seleccionadas. Estas variables ("famrel", "absences", "G2") serán utilizadas como nodos de entrada en la capa de entrada de la red neuronal.

La determinación de la cantidad de nodos en la capa oculta es un factor crítico para el éxito del entrenamiento de la red neuronal. No existe una cantidad predefinida de nodos para esta capa, ya que tanto un número insuficiente como un número excesivo pueden afectar negativamente el desempeño del modelo. Un número reducido de nodos puede limitar la capacidad de aprendizaje de la red, mientras que un exceso de nodos puede conducir al fenómeno de sobreajuste, en el cual el modelo se adapta demasiado a los datos de entrenamiento, perjudicando su rendimiento con nuevos datos.

Por lo tanto, se optó por seleccionar diez nodos para la capa oculta, considerando un equilibrio entre la capacidad de aprendizaje y la prevención del sobreajuste. El código utilizado fue el siguiente:

Figura 8. Código fuente de red neuronal

Es importante recordar que para construir la red neuronal, el paquete `nnet` emplea la función sigmoidea logística para la activación de la capa oculta, y el algoritmo BFGS (Broyden-Fletcher-Goldfarb-Shanno) para el entrenamiento del modelo.

Para visualizar gráficamente la arquitectura de la red neuronal, se hizo uso de la función `plotnet` proporcionada por el paquete NeuralNetTools. Esta representación gráfica permite una comprensión visual de la estructura de la red, incluyendo la disposición de las capas y las conexiones entre los nodos. La red neuronal se puede observar en la siguiente figura:

Figura 9. Red neuronal propuesta

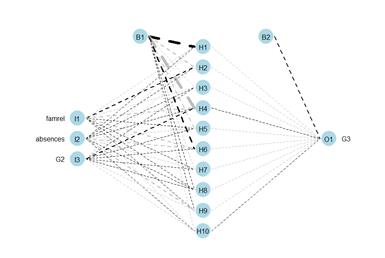
Una vez construida la red neuronal, se procedió a evaluar la validez del modelo utilizando el conjunto de datos de prueba, que comprende el 15% del total de los datos. El resultado de esta evaluación se presenta en el siguiente gráfico:

Figura 10. Comparación de datos de entrenamiento y prueba

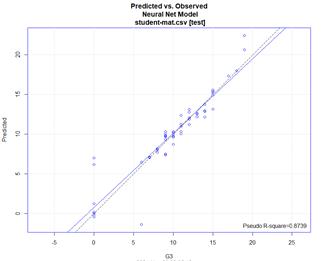
Como se puede ver en el gráfico, este modelo tiene un 87% de efectividad en la predicción del rendimiento académico de un estudiante (Pseudo R-square=0.8739).

Con el fin de investigar sobre la eficacia de este modelo de predicción basado en redes neuronales, se lo comparó con un modelo de regresión lineal múltiple. El código para ejecutar un modelo de regresión lineal múltiple fue el siguiente:

Figura 11. Código fuente de regresión lineal múltiple

Con este modelo, se obtuvo un pseudo R2 de 0.8152 (81%), lo que indica que la red neuronal supera en eficacia a un modelo de regresión lineal múltiple en la predicción del rendimiento académico.

En resumen, los pasos seguidos en esta investigación fueron los siguientes:

1. Se adquirió un conjunto de datos de una institución educativa, que incluía diversas variables de diferentes categorías, como académicas, sociodemográficas, entre otras.
2. Se realizó un análisis de las variables con el fin de identificar aquellas con mayor influencia en el rendimiento académico dentro del contexto de los datos obtenidos.
3. Tras llevar a cabo un análisis de eliminación retroactiva, se determinó que tres variables poseen un valor-p mínimo, lo que indica una alta incidencia en la nota final, la cual puede corresponder a aprobación o reprobación. Estas variables son: "famrel" (calidad de la relación familiar), "absences" (número de ausencias en la institución) y "G2" (notas de matemáticas del segundo periodo).
4. Utilizando estas variables como datos de entrada, se construyó una red neuronal para predecir el rendimiento académico de un estudiante, es decir, determinar si obtendrá una nota de aprobación o no.
5. Finalmente, se validó la red neuronal con el conjunto de datos de prueba, logrando una efectividad del 87% en la predicción del rendimiento académico de los estudiantes.

DISCUSIÓN

La capacidad de predicción es una herramienta invaluable en diversos campos, incluido el educativo, donde puede contribuir significativamente a la planificación y ejecución de actividades destinadas a evitar la deserción escolar. En esta investigación, se empleó la potencialidad de las redes neuronales para prever el rendimiento académico de los estudiantes, logrando una efectividad del 87%.

La arquitectura de la red neuronal consistió en tres neuronas en la capa de entrada, diez nodos en la capa oculta y un nodo en la capa de salida. Se utilizó el paquete nnet de CRAN, el cual emplea la función sigmoidea logística para la activación de la capa oculta y el algoritmo BFGS para el entrenamiento del modelo.

El alto porcentaje de predictabilidad alcanzado del 87% proporciona un sólido respaldo para continuar con esta línea de investigación y avanzar hacia la fase de despliegue del modelo. En esta etapa, se podría considerar la integración del modelo en una página web o una aplicación móvil para que pueda ser accedido y utilizado por los interesados. Este enfoque permitiría aprovechar las ventajas de la predicción del rendimiento académico de manera más amplia y accesible.

Durante muchos años el rendimiento académico ha sido, y sigue siendo, un campo que ha suscitado el interés de muchos investigadores en muy distintas especialidades. Tiene varias repercusiones, como por ejemplo: un rendimiento académico elevado permite acceder a estudios superiores de mayor prestigio y de futuro más prometedor; y, por otro lado, un bajo rendimiento provoca que muchos estudiantes lo abandonen, con las consecuencias personales adversas que esto conlleva: malas perspectivas laborales y económicas, autoestima deteriorada, etc. Una gran cantidad de trabajos investigadores verifica que existe un patrón consistente que permite adivinar el rendimiento académico, lo que se puede definir como los factores que lo explican. Asimismo, se ha desarrollado una gran cantidad de trabajos orientados a formalizar mecanismos para predecir el rendimiento académico, denominándolos modelos de predicción del rendimiento académico. (Andreu et al., 2020) (Valenzuela et al., 2023)

El cerebro humano tiene un número muy elevado de neuronas, superior a cien mil millones. Entre estas neuronas existen conexiones llamadas sinapsis, de las cuales hay también cientos de miles de millones. Una neurona individual no parece presentar un comportamiento reflexivo, pero un gran número de ellas, interconectadas, pueden presentar un comportamiento graduado. Cada neurona tiene una serie de ramificaciones, en cada una de las cuales recibe un sin número de señales procedentes de otras neuronas. Cuando el potencial generado alcanza determinado valor, se dispara el potencial de la neurona, con lo que se inician una serie de fenómenos que desembocan en la emisión de un potencial de acción. Las conexiones se realizan entre la membrana de la neurona y los filamentos de unas de estas ramificaciones: las dendritas. Las señales se tratan en una zona de la neurona llamada soma, y desde allí se envían señales a otra ramificación, el axón. Las señales circulan a lo largo del axón y se transmiten a muchas neuronas según terminales. (Paúl, 2022)

En las redes neuronales se aplican otros mecanismos de conexión e interacción de los que presentamos: ninguna interconexión de una red neural es crucial, y por tanto la capacidad de "aprendizaje" de la red neural, de adaptarse a las circunstancias cambiantes, permite un cierto paralelismo con el cerebro humano. Habitualmente aplicamos los conocimientos que tenemos sobre las neuronas biológicas para definir ciertos procesos de interconexión, adaptabilidad... de manera que tratamos de describir, de modelar estos comportamientos a través de los ordenadores. Uno de los problemas que surgen es el de la ponderación: una de las neuronas, por sí sola, no parece tomar demasiadas decisiones. Sin embargo, si le sumamos muchos vecinos, entonces sí se puede "aprovechar" toda esa sabiduría colectiva y tomar una decisión. (Paredes-Robles et al., 2023)

CONCLUSIONES

Como conclusiones de este estudio, se puede resaltar los siguientes aspectos:

Este estudio demostró que las redes neuronales son una herramienta efectiva para predecir el rendimiento académico de los estudiantes, alcanzando una precisión del 87%. Este alto nivel de predictibilidad respalda la utilidad de este enfoque en la identificación temprana de estudiantes en riesgo de deserción escolar.

Se identificaron tres variables clave que influyen significativamente en el rendimiento académico: la calidad de la relación familiar (famrel), el número de ausencias en la institución (absences) y las calificaciones de matemáticas en el segundo periodo (G2). Estas variables proporcionaron la base para la construcción del modelo de red neuronal.

La comparación con un modelo de regresión lineal múltiple reveló que la red neuronal supera en eficacia al modelo tradicional, con un pseudo R2 del 87% frente al 81% del modelo de regresión lineal. Esto subraya la superioridad de las redes neuronales en la predicción del rendimiento académico.

Considerando la alta efectividad del modelo de red neuronal, se recomienda avanzar hacia la fase de despliegue del modelo. Integrar el modelo en una plataforma en línea, como una página web o una aplicación móvil, permitirá su acceso y uso por parte de profesores, administradores educativos y estudiantes, facilitando así la identificación y el apoyo a los estudiantes en riesgo.

A pesar del éxito inicial, es crucial continuar validando y refinando el modelo a medida que se recopilen más datos y se realicen nuevas investigaciones. Esto garantizará que el modelo siga siendo relevante y preciso en entornos educativos cambiantes. Aunque se identificaron variables importantes en este estudio, se recomienda explorar la inclusión de otras variables potencialmente relevantes, como el contexto socioeconómico, el apoyo familiar y la participación en actividades extracurriculares, para mejorar aún más la capacidad predictiva del modelo.

Dada la complejidad y la multidimensionalidad del rendimiento académico, se sugiere colaborar con expertos en psicología educativa, sociología y otras disciplinas relacionadas para obtener una comprensión más completa de los factores que influyen en el éxito académico y en la deserción estudiantil. En conjunto, estas conclusiones y recomendaciones apuntan hacia la utilidad y el potencial de las redes neuronales en la mejora de la predicción del rendimiento académico y la mitigación de la deserción estudiantil, contribuyendo así a la excelencia educativa y al bienestar estudiantil.

REFERENCIAS

Andersen, B., Mizoguchi, Y., Fukumoto, Y., Broadbridge, P., Polthier, K., Saeki, O., y Kamiyama, N. (2017). The Role and Importance of Mathematics in Innovation. Singapure: Springer.

Buckingham, S. (2012). UNESCO Institute for Information Technlogies in Education. Obtenido de https://iite.unesco.org/publications/3214711/

Caicedo Bravo, E., y López Sotelo, J. (2009). Una aproximación práctica a las redes neuronales artificiales. Santiago de Cali: Programa Editorial Universidad del Valle.

Flóres López, R., y Fernandez, J. (2008). Las Redes Neuronales Artificiales. España: Gesbiblio S.L.

Gandrud, C. (2015). Reproducible Research with R and RStudio. Berlin: CRC Press.

Gardener, M. (2012). Beginning R: The Statistical Programming Language. United States: John Wiley and Sons.

Graupe, D. (2013). Principios de redes neuronales artificiales (Vol. 7). World Scientific. https://books.google.es/books?hl=es&lr=&id=Zz27CgAAQBAJ&oi=fnd&pg=PR7&dq=Graupe,+D.+(2013).+Principles+of+Artificial+Neural+Networks.+United+States:+World+Scientific+Publishing,+Co.&ots=wHbiTDTRMN&sig=aqzjh0VDh8wIf8wIMv4X8KKs12U

Heaton, J. (2012). Math of Neural Networks. United States: Heaton Reacher, Inc.

Hidalgo, S., Maroto, A., y Palacios, A. (2004). ¿Por qué se rechazan las matemáticas? Analisis Evolutivo y Multivariante de Actitudes Relevantes hacia las Matemáticas. Revista Educación.

Incio, F., Capuñay Sanchez, D., Estela Urbina, R., Delgado Soto, J., y Vergara Medrano, S. (2021). Diseño e Implementación de una Red Neuronal Artificial para predecir el rendimiento académico en estudiantes de Ingeniería Civil de la UNIFSLB. Veritas Et Scientia, 11.

Longoni, M., Porcel, E., López, M., y Dapozo, G. (2010). Modelos de Redes Neuronales Perceptrón Multicapa y de Base Radial para la predicción de rendimiento académico de alumnos universitarios. XVI Congreso Argentino de Ciencias de la Computación, 10.

Macías Moles, Y. (2021). La tecnología y la Inteligencia Artificial en el sistema educativo. Universitat Jaume I, 54.

Matich, D. J. (2001). Redes Neuronales: Conceptos básicos y aplicaciones. México: Universidad Tecnológica Nacional.

Ocaña Fernandez, Y., Valenzuela Fernandez, L., y Garro Aburto, L. (2019). Inteligencia artificial y sus implicaciones en la educación superior. Propósitos y Representaciones, 536-568.

Pawlus, M., y Devine, R. (2020). Hands-On Deep Learning. Birmingham: Packt Publishing Ltd.

Porcel, E., Dapozo, G., y Lopez, M. (2009). Modelos predictivos y técnicas de minería de datos para la identificación de factores asociados al rendimiento académico de alumnos universitarios. XI Workshop de Investigadores en Ciencias de la Computación, 635-639.

Salgado Reyes, N., Beltrán Morales, J., Guaña Moya, J., Escobar Terán, C., Nicolalde Rodriguez, D., y Chafla Altamirano, G. (2018). Model to predict academic performance based on neural networks and learning analytics. Revista Ibérica de Sistemas y Tecnologías de la Información, 10.

Sanchez Vila, E., y Lama Penin, M. (2007). Técnicas de la Inteligencia Artificial Aplicadas a la Educación. Revista Iberoamericana de Inteligencia Artificial, 7-12.

Shafique, U., y Qaiser, H. (2014). A Comparative Study of Data Mining Process Models (KDD, CRISP-DM and SEMMA). International Journal of Innovation and Scientific Research, 6.

Zambrano Matamala, C., Rojas Diaz, D., Carvajal Cuello, K., y Acuña Leiva, G. (2011). Análisis de rendimiento académico estudiantil usando data warehouse y redes neuronales. Ingeniare. Revista Chilena de Ingeniería, 14.

Andreu, M. E., Pareja, R. M., & Gelabert, A. S. (2020). Aspiraciones ocupacionales y expectativas y elecciones educativas de los jóvenes en un contexto de crisis. RES. Revista Española de Sociología, 29(3), 27-46. unirioja.es

Valenzuela, J. P., Kuzmanic, D., Villalobos, C., & Quaresma, M. L. (2023). Cambio y recomposición social en universidades y carreras de élite en Chile (2009-2019). Estudios Pedagógicos, 49(3), 63-84. 146.83.217.169

Paúl, E. R. (2022). Ideas sobre la Divinidad. Mayéutica Revista Científica de Humanidades y Artes, 10(1), 57-72. uclave.org

Paredes-Robles, K. J., Vélez-Pincay, J., & Marin-Llaver, L. R. (2023). Estrategia Educativa para mejorar el rendimiento académico en estudiantes de bachillerato. MQRInvestigar, 7(3), 3204-3219. investigarmqr.com